Design an all-digital modulator with an RF output | Soukacatv.com

A software-defined radio (SDR) terminal promotes programmable realizations of the physical layer functionalities. A lot of research work has been done in applying DSPs and FPGAs to implement the baseband functionalities of the physical layer.

An SDR is defined as a radio in which the digitization is performed at some stage downstream from the antenna. Then the radio can use flexible and reconfigurable functional blocks to implement the DSP algorithms. As technology advances, the digitization might be at, or very close to the antenna, such that almost all the radio functionalities are realized through software using a high-speed, reprogrammable DSP engine.

HDMI Encoder Modulator,16in1 Digital Headend,HD RF Modulator at Soukacatv.com

Current radios combine analog and digital building blocks. The RF functions are most likely being implemented using analog circuits, while the baseband functions are more suitable for DSP implementations. A digital front end (DFE) is often used to bridge between the RF and baseband processing. The DFEs are normally capable of processing signals with frequencies at about tens of megahertz, often called digital intermediate frequencies (IF). Hence, significant analog blocks remain between the RF and digital IF.

Digital RF transceivers can extend the software defined functions into radio frequencies. The key advantages of all digital transmitters are high-efficiency power amplification; digitally combining signals from multiple channels; and software programmability or reconfigurability.

Using an all digital transmitter, the entire transmitter can be realized using a DSP or FPGA, which can take advantage of the increasing performance of CMOS technology. Besides its compatibility with SDR, DSP-based RF systems can be made to compensate for the RF channel's impairments. Therefore, digital signal generation directly at radio frequency has drawn a lot of interests among researchers and engineers.

One of the more traditional methods uses band-pass delta-sigma modulation to generate binary signals at radio frequency. Binary signaling can be used with switch-mode power amplifiers (PAs) to achieve higher efficiency compared to other PA technologies ((Fig. 1). The drawback of this architecture is that the band-pass delta-sigma (BPDS) modulator runs at four times the center frequency, which can be several gigahertz. To accommodate such high frequency operation, custom ICs must be carefully designed, which lack reprogrammability.

Another method uses pulse width modulation (PWM) to digitally synthesize binary RF signals. PWM was long ago introduced as an analog modulation, but has gained popularity recently, especially in the digital audio amplification applications. Class D audio PAs, driven by PWM audio signals, can achieve efficiency above 90%. Delta-sigma type modulation can also be used in digital PWM, but operates at a lower frequency compared with the BPDS method. However, the delta-sigma loop tends to be more complicated compared to BPDS because of the low over-sampling ratio and the non-linearity associated with PWM.

The test setup uses signal sources computed offline that are stored in pattern generator. In this example, a real-time system was designed to demonstrate the capabilities of digital generation of RF signals using digital PWM.

Digital RFPWM generation
Digital PWM was motivated by the digital PA technique, by which a digital signal can be converted directly into high-power analog signals without intermediate digital to analog converter (DAC) stages. The digital PA has gained some popularity in digital audio applications, due to the increasing interest to develop all digital audio system.

In digital PWM, the pulse widths are quantized with respect to a high-speed clock. Therefore, a simple counter can be used to generate the digital PWM waveform based on the high-speed reference clock (Fig. 2). The interpolator increases the sampling frequency of the PCM input to a frequency suitable for performing PWM modulation. This frequency is often called the pulse repetition frequency (PRF).

The natural sampler calculates the naturally sampled signal values based on the uniformly sampled digital signal. It's been shown that a naturally sampled signal experiences far less baseband distortion comparing to uniformly sampled signal, when PWM is performed.

Quantization is needed to ensure that the high-speed reference clock runs at a reasonable frequency for implementation purpose. For example, if the original PCM input is 44.1 kHz, a 16X interpolator will result in a PRF of 705.6 kHz. The high-speed reference clock must have a 46-GHz frequency if the pulse width is quantized to 16 bits. If only 8 bits are needed to quantize the pulse width, the high-speed reference clock's frequency can be reduced to 180 MHz. Therefore, makes it's easier to implement using moderate technology. A noise-shaping technique, such as delta-sigma modulation, can be used to suppress the baseband noise introduced by quantization.

The processing intensive blocks, natural sampler, and quantization with noise shaping, have the sampling frequency of PRF. This is the main motivation of this work—the main signal-processing algorithms are executed at the lower PRF rather than the RF. To accommodate the bandwidth requirement in the QAM modulator, this difference is 100 MHz versus several GHz.

All digital RFPWM
An all digital RF PWM is called quadrature integral noise shaping (INS, which is an algorithm used in the quantization and noise-shaping block. Its main goal is to suppress the noise power in the baseband introduced by the pulse width quantization process. It differs from other algorithms by introducing non-linear terms into the feedback loop. Without considering the details of the INS algorithm, the quadrature INS can be viewed as two individual PWM modulators for the in-phase (I) and quadrature (Q) paths of complex signals respectively.

These PWM modulations use the same architecture as previously described. The outputs from these PWM are baseband signals that need to be further mixed with digital local oscillator signals to form band-pass signal at RF. If both the baseband PWM signals and the digital local oscillator signals are binary, this mixing operation is nothing more than a simple logic XOR operation.

Another method to simplify this mixing operation is to make the in-phase LO take these ternary values of 0, 1, 0, -1, while the quardrature LO takes the values of -1, 0, 1, 0. Therefore, the digital mixer only outputs -Q, I, Q, -I in sequence. When both I and Q are binary PWM signals, the mixer's output will also be binary. To make sure the LO signals have one of these two formats, the sampling frequency must be at 4X the LO frequency. The signals from two digital mixers are then combined to form the desired signal at RF.

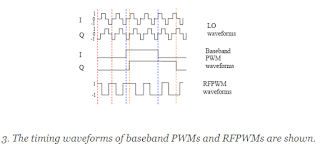
For a signal modulated using PWM, the signal information is carried in the width of the pulse. Because pulse width is defined by the duration from the rising edge to the falling edge, the transition edges should be preserved after the baseband PWM. However, a 90-degreee phase difference exists between the in-phase and quadrature LO signals. Hence, extra care must be taken to ensure that the baseband PWMs are synchronized with their LO signals respectively. Because the sampling rate is set at 4X the LO frequency, the phase difference is equal to one quarter cycle-time difference.

The baseband PWM waveforms for in-phase and quadrature are constructed differently: there's an intentional quarter-cycle difference introduced to compensate for the phase difference between the in-phase and quadrature LO singals. Looking at the timing waveforms of baseband PWMs and RFPWMs, the LO signals take the ternary format, and the combined output RFPWM signal is binary. In addition, both baseband PWMs are synchronized to the rising edges of their LO signals respectively.

The QAM-PWM modulator discussed here uses the quadrature PWM architecture, while the INS algorithm isn't chosen due to its high computational requirement. A non-recursive noise shaping method is used instead.

Digital PWM noise shaping
Noise shaping has been widely adopted in over-sampled data converters. The purpose of noise shaping is to generate coarsely quantized signals instead of finely quantized signals, while preserving the SNR performance within a limited bandwidth. In the digital PWM system, noise shaping is necessary as the reference clock would have been at a very high frequency had the pulse width been finely quantized, e.g., using 16 rather than 8 bits when the PRF is 705.6 kHz.

The noise shaping filters used in traditional data converters have been well studied, and most methods can also be used in the digital PWM. But the noise shaping behavior in the digital PWM differs from traditional DACs, due to the non-linear effects introduced by the PWM.

A simulation model compares the noise shaping performance between PWM and traditional DAC (Fig. 4). The digital PWM and traditional DAC use the same noise shaping filter and quantizer. The noise transfer functions (NTF) used in this simulation are specified by H(z) = (1-z-1)N, where N ranges from 1 to 5. This type of noise shaping filter is not optimal as far as the in-band noise suppression performance is concerned, but it is sufficient to demonstrate the different behaviors between the PWM and a traditional DAC. The effects of analog components in the DAC aren't included in the simulation; only the all digital noise shaping loop is considered. The following parameters were selected for the simulation:

Frequency of the input single tone signal = 11 kHz Baseband bandwidth = 20 kHz Sampling frequency = 705.6 kHz Input signal level = -6 dBFS Quantization levels = 64

For traditional DACs, the quantization levels indicate the number of bits used in the final DAC, while for PWM, this refers to the number of high-speed clock edges in each pulse cycle (Table 1).

The SNR measurements are almost identical between the PWM and the traditional DAC when the lower order NTFs are used, i.e., N = 1 and N = 2. When the order of NTF is increased, the SNR trend for PWM differs from traditional DAC. Note that: the PWM SNR may not be improved as rapidly as a traditional DAC when N is increased from 2 to 3; and the PWM SNR deteriorates when N is further increased to 4 and 5.

The quantization noise might be folded back to the baseband if the NTF's gain is high at the high frequency. This can be explained by the non-linearity nature of the PWM modulation. However, this non-linearity effect can be neglected if only moderate baseband SNR performance is required. Through this simulation model, we formulated our criteria to design a non-recursive NTF filter used for a digital PWM system. That criteria includes minimizing the ratio between baseband energy and total energy when the filter's input is white noise. The filter coefficients should satisfy minimum phase, one-norm requirement, and its first coefficient should be unity. The filter gain at high frequency should be limited.

These criteria can then be formulated mathematically as follows. Assume an N-tap FIR filter with coefficients h, where h = (h0, h1, …, hN-1)T, the baseband energy can be calculated by

wherein R is a matrix, and

The total energy can be calculated using Parseval’s theorem,

Therefore the optimized NTF should try to minimize

The parameters α and β are used as weighting factors when performing the optimization. The object function should be minimized subject to the condition that the one-norm of h should be bounded, which is dependent on the number of levels in the quantizer, i.e.,

The filter should be minimum phase, meaning that all the zeros of the filter should be within the unit circle. The gain at high frequency should be bounded, such that

The all-digital transmitter to be demonstrated is specified to have 10-MHz baseband bandwidth, and the PRF is chosen to be 100 MHz. The center frequency is 800 MHz; therefore the frequency of the high-speed reference clock is 3.2 GHz. The prototype implementation uses an eight-tap finite impulse response (FIR) NTF designed using this method.

Hardware prototyping and measurements
As described, all the signal processing algorithms required by the digital PWM is running at the frequency of the PRF. The only high-speed circuit required is the final PWM waveform generation. Therefore, it's feasible to prototype an all digital QAM-PWM modulator on an off the shelf FPGA device.

In the architecture of the digital QAM-PWM modulator, the quadrature path should consist of almost identical architectural blocks (Fig. 5). The QAM modulator consists of one QAM symbols generator whose symbol rate is 5.057 MHz, one interpolation filter to up-sample the sampling rate to 16X the symbol rate, and one converter that converts the sampling rate to the 100 MHz PRF.

The digital PWM consists of one natural sampler, one quantization with noise shaping block, and one PWM waveform generator. The natural sampling algorithm consists of only feed-forward data-paths; therefore it can be pipelined fairly easily. The quantization with noise shaping block has feed-back paths; therefore it's more difficult to implement even though the PRF is merely 100 MHz.

The FIR NTF filter is realized using the transposed structure, combined with the retiming technique and canonic signed digit (CSD) conversion of some coefficients. The mixing between LO signals and all the possible baseband PWM signals were pre-computed and stored in a ROM. This ROM is addressed by the quantization output, i.e., the quantized pulse width. The selected RF PWM waveforms from the in-phase and quadrature paths will be combined before the high-speed serializer generates the 1-bit RF signal.

The FPGA device chosen for the prototype is Xilinx's Virtex2pro, model XC2VPX20-FF896, speed grade -7. This part has an on-chip multi-gigabit transceiver, which is used as the high-speed parallel-to-serial converter to generate a binary signal at 3.2 GHz (Table 2).

The logic elements allocation results are extracted from Synplcity synthesis results. The final place and route tool reports that the entire QAM-PWM design utilizes 18 multipliers (20%), four RAM16s (4%), and 3911 slices (39%). Note: the number in parentheses is the percentage with respect to the total available resources on this FPGA.

While the pass-band noise floor is about 45 dB down from the signal, a more aggressive noise shaping technique can help achieve better pass-band noise performance. However the computation requirement for that case might prevent it from being implemented; using an off-the-shelf FPGA will be difficult. The EVM measurement is less than 1%, which is almost identical to the EVM measured at the output of QAM.

Established in 2000, the Soukacatv.com main products are modulators both in analog and digital modulators, amplifier and combiner. We are the very first one in manufacturing the headend system in China. Our 16 in 1 and 24 in 1 now are the most popular products all over the world.

For more, please access to https://www.soukacatv.com.

Source: eetimes